자바스크립트의 숫자(Number)형 (Feat. 부동 소수점 vs 고정 소수점)
맨날 까먹어서 정리하는 내용 ...

자바스크립트에서의 숫자는 다른 언어와 달리 하나의 숫자 타입만 가진다.
Number
ECMAScript 사양에 따르면, 숫자 타입의 값은 배정밀도 64비트 부동소수점 형식을 따른다.
모든 수를 실수로 처리하며, 정수를 표현하기 위한 데이터 타입이 별도로 존재하지 않는다.
배정밀도 64비트 부동소수점은 무엇일까 ?
컴퓨터에서 실수를 표현하는 방법에는 크게 4가지가 있다.

컴퓨터가 소수점 아래 숫자가 있는 실수를 표기할 때,
소수점의 위치를 고정시켜 표현하는 방식을 고정소수점,
소수점의 위치를 고정시키지 않고 가수와 진수를 이용하는 방식을 부동소수점 이라 한다.
1. 단정밀도/배정밀도 고정소수점 방식
단정밀도 고정소수점 방식은 소수를 아래처럼 표현한다.
[ 0 000000000000000 0000000000000000 ]

그러면 -2.75 를 단정밀도 고정소수점 방식으로 표현해보자.
음수 이므로, 맨 앞 비트는 1
정수부 2는 이진수로 10, 따라서 000000000000010
0.75은 이진수로 어떻게 표현할까 ?
정수부에서 자리가 올라갈 수록 2의 거듭제곱 형태로 표현하는 반면,
소수부에서는 자리가 내려갈수록 1/2의 거듭제곱 형태로 표현한다.
0.1 = 0.5
0.01 = 0.25
0.001 = 0.125
...
형태로 표현한다.
소수를 이진수로 바꾸는 방법은 해당 소수에 2를 곱하면서
그 결과가 1로 떨어질 때까지 혹은 똑같은 소수점이 나올 때까지 반복하면 된다.
0.75 * 2 = 1.5
0.5 * 2 = 1.0
결론적으로 0.11이 되고
-2.75 는 단정밀도 고정소수점 방식으로 1 000000000000010 1100000000000000 이 된다.
해당 방식은 제한된 자릿수 때문에 표현할 수 있는 범위가 굉장히 작다. (배정밀도도 마찬가지)
이를 보완하기 위해 나온 방식이 부동소수점 방식이다.
2. 단정밀도/배정밀도 부동소수점 방식
부동소수점 방식은 소수점이 고정되어 있지 않고 좌우로 움직일 수 있는 방식이다.
따라서 소수점이 고정되어 있는 것보다 다양한 수의 표현이 가능하다.
크게 지수부와 가수부로 나뉘는데,

단정밀도의 경우에는 지수부가 8bit, 가수부가 23bit이며
배정밀도의 경우에는 지수부가 11bit, 가수부가 52bit이다.

부호부 (Sign) : 1비트. 숫자의 부호를 나타낸다.
지수부 (Exponent) :8비트. 지수를 나타낸다.
가수부 (Mantissa) : 23비트. 가수 또는 유효숫자를 나타낸다.
그러면 2.75를 단정밀도 부동소수점 방식으로 표현해보자.
먼저 2.75를 2진수로 변환하는 과정이 필요하다.
앞서 했던 방식으로 2.75 = 10.11(2) 형태가 된다.
그다음 이진수의 소수점을 이동시켜 소수점 왼쪽에 1만 남도록 만든다. (정규화 과정)
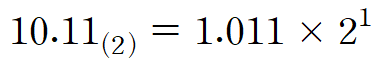
그 후 지수부인 1을 8bit에 바로 대입하는 것이 아니라
바이어스(bias) 값을 더해줘야 한다. (지수가 음수가 될 수도 있기 때문에)
* 32bit IEEE 754 형식에는 bias가 고정값 127, 64bit에서는 1023이다. 2^(k-1) 값 (k는 지수 비트수)
그러면 1 + 127 = 128 이고
해당 값을 2진수로 바꿔주면 10000000 이고, 소수점 011은 가수부 왼쪽부터 채워준다.
최종적으로 표현하면
0 10000000 01100000000000000000000
이 된다.
하지만 부동소수점 방식은 제한된 길이 64bit 안에 긴 소수점까지도 표현해야되기에 근삿값을 사용한다.
따라서 부동소수점으로 표현된 소수는 정확한 값이 아니라는 것이다.
개발자 도구 콘솔창에 0.1+0.2 == 0.3 을 쳐보면 어떤 값이 나올 것 같은가 ?
상식상으로는 true지만, 해당 표현식의 값은 false다.

그 이유는
0.1 을 이진수로 표현했을 때 순환소수 형태(0.00011001100...)이기 때문에 정확하게 표현할 수 없다.
(순환 소수 형태는 부동소수점으로 표현할 때 가수부 53번째 비트에서 반올림 하여 표현한다)
따라서 정확한 0.3값을 계산할 수 없기 때문에 false를 출력한다.
3. 자바스크립트에서 소수점를 정확히 계산하는 방법?
그러면 자바스크립트에서 어떻게 소수점를 정확히 계산하여 표현할 수 있을까 ?
크게 2가지 방법이 있다.
1) toFixed() 메서드
toFixed()는 입력받은 숫자를, 매개변수만큼 자리수를 반올림해 String으로 반환해주는 함수이다.
매개 변수는 0~20까지 입력가능하며 2로 입력했을 때 소수점 둘째자리에서 반올림하여 나타낸다.
let result = (0.1 + 0.2).toFixed(2);
// '0.30'
Number(result);
// 0.3반환 형태가 String 형태인 것만 주의하자!
2) Math.round() 메서드
Math.round() 또한 반올림을 해주는 함수이다. 매개변수로 들어온 값을 반올림한 후, 가장 가까운 정수 값을 반환한다. toFixed()의 매개변수를 0으로 지정해줬을 때처럼 정수값을 반환해준다는 점에 주의해야 한다.
Math.round(30.29);
// 30
Math.round((0.1 + 0.2) * 10) / 10;
// 0.3
+ 자바스크립트의 수 범위
자바스크립트의 수의 범위는 (2 ^ 53 - 1) ~ -(2 ^ 53 - 1) 이다.
= 9007,199,254,740,991 ~ -9,007,199,254,740,991
해당 수를 넘어가게 되면 연산결과가 부정확한 값이 나온다.
(64비트 부동 소수점 수의 정밀도는 정수부는 15자리까지, 소수부는 17자리까지만 유효하다)
참고 링크
https://hbsowo58.tistory.com/460- 소수점을 2진수로 변환하는 법
https://woo-dev.tistory.com/93 - 소수점을 2진수로 변환하는 법
https://m.blog.naver.com/7rlaguswns7/221349728794 - 부동소수, 고정소수점
https://kangdy25.tistory.com/51 - 부동소수 고정소수
https://www.h-schmidt.net/FloatConverter/IEEE754.html 부동소수점 변환기